Wie letztens geschrieben, sind die Implikationen von Big Data (mindestens) einen eigenen Artikel wert. In diesem dreht es sich darum, was für Gefahren von Big Data und der (automatisierten) Verarbeitung potentiell ausgehen. Und warum es dringend notwendig ist, neben den technischen auch ethische und moralische Diskussionen zu führen.
Wie letztens ausgeführt, können Machine Learning (ML) und Künstliche Intelligenz (KI) als notwendige Werkzeuge für den Umgang mit Big Data gesehen werden. Erst durch deren Entwicklung wird es möglich, dass aus der schieren Masse an Daten tatsächlich Informationen gewonnen und neue Erkenntnisse gezogen werden. Und umgekehrt brauchen ML & KI riesige Datensätze um überhaupt funktionieren zu können.
Die Grundidee hinter ML & KI ist, dass sogenannte „selbstlernende Algorithmen“ (Computerprogramme) mit einer riesigen Menge an Information gefüttert werden und dadurch selbst Zusammenhänge erkennen lernen. Zum Beispiel werden dem Computerprogramm eine Million Tierfotos gefüttert – zusammen mit der Bezeichnung des Tieres auf den Fotos (Hund, Katze, Löwe, Gorilla, …). Nach diesem „Training“ ist das Computerprogramm in der Lage selbständig neue Fotos zu klassifizieren, also das jeweilige Tier zu benennen – im Idealfall.
Idealfall deshalb, weil das nicht immer so perfekt und einfach funktioniert. Nun ist gerade der Vorteil von selbstlernenden Algorithmen ihre größte Schwachstelle: sie sind selbstlernend. Es weiß daher am Ende niemand wie und warum das Programm zu seiner Entscheidung gekommen ist. Sie sind Black Boxes. Und wie gezeigt wurde sind diese Algorithmen durchaus anfällig für Manipulationen. Natürlich ist an dieser Stelle der Einwand berechtigt, dass niemandem ein Stein aus der Krone fällt, wenn dank KI Omas Stubentiger fälschlich als König der Löwen oder Dackel klassifiziert wird. Aaaaaber…
Was, wenn es sich nicht (nur) um Tierfotos handelt die von KI verarbeitet und klassifiziert werden? Eines der berühmtesten Beispiele für fehlerhafte Klassifikation lieferte Google, als ihre Foto-App einen Schwarzen und seine Freundin als Gorillas klassifizierte. Ein ähnlicher Fehler unterlief Apple beim Entsperren des iPhones mittels FaceID, ein Feature das bei nicht-weißen Personen (Latinos, Asiaten, Schwarze, …) deutlich schlechter funktionierte.
Hier zeigte sich bereits eine deutliche Schwachstelle der KI: sie wird höchstens so gut wie die Trainingsdaten mit denen sie gefüttert wird. Und es hängt von den EntwicklerInnen ab, was für Trainingsdaten den Programmen serviert werden.
Nun kann man als böswilliger Mensch sogar diesen höchst peinlichen (und rassistischen) Fehlern „es kam ja niemand wirklich zu Schaden“ entgegenhalten. Was aber, wenn KI in (deutlich) relevanteren Gebieten zum Einsatz kommt? Zum Beispiel bei der Vergabe von geförderten Wohnungen, der Suche nach MitarbeiterInnen oder der Bonitätsprüfung durch Banken? Übrigens alles bereits tatsächliche Anwendungen.
Dazu muss man sich zuerst die Frage stellen, was für Daten verarbeitet werden und woher sie kommen. Wie spätestens seit dem Facebook-Cambridge-Analytica-Skandal (hoffentlich) bekannt ist, werden von jedem von uns extreme Mengen an Daten gesammelt. Und zwar von allen möglichen (und unmöglichen) Seiten. Dazu gehören neben Facebook und anderen neuen Sammlern wie Amazon, Google und online-Werbeagenturen auch die „klassischen“ Datensammler wie Gläubigerschutzverbände, Banken, Supermärkte (Kundenkarten!) oder auch die gute, alte Post. Und inzwischen ist das Datensammeln und Zusammentragen ein eigenes, lukratives Geschäft.
Diese (oft dubiosen) Firmen kaufen Nutzerdaten aus allen (oft dubiosen) Quellen derer sie habhaft werden können und tragen diese zusammen (z.B. Echt-Name, E-Mail-Adresse, Twitter-Account, Geburtsdatum, Wohn-Adresse, Kreditwürdigkeit, Vorstrafen, Sozialversicherungsnummer, …) um sie dann Paketweise an Anwender (z.B. Personalfirmen für automatisiertes MitarbeiterInnen-Screening) weiter zu verkaufen. Und wie werden diese Daten unterschiedlichster Quellen einer eindeutigen Person zugeordnet? Oft per Geburtsdatum und Name.
Klingt plausibel? Ist es aber bei weitem nicht.
Das Geburtstagsparadoxon
Hinweis: Es folgt ein wenig Mathematik (bzw. Statistik). Ich habe versucht die einzelnen Schritte sehr verständlich zu halten. Sollte deine Aversion wirklich zu groß sein um sie zumindest zu überfliegen, dann lies ab dem letzten Absatz dieses Abschnittes weiter.
Angenommen, 2 zufällige Menschen begegnen sich in einem Raum. Dann sind ihre Geburtstage zufällig im Jahr verteilt (*s. Anm. unten). Diese zufällige Verteilung können wir nachbauen indem wir 365 Zettel mit den Zahlen 1 bis 365 in eine Schüssel legen, einen Zettel ziehen, diesen wieder hineinlegen und dann ein zweites Mal einen der 365 Zettel ziehen.
Für unsere 2 Personen gibt es eine mögliche Anzahl von 133.225 Geburstagskombinationen. Diese kommt wie folgt zustande:
Kombination 1 ist, wenn Person A am 1. Tag Geburtstag hat und Person B ebenfalls am 1. Tag. Für eine übersichtlichere Darstellung wollen wir dafür die formale Schreibweise 1 – 1 einführen.
Kombination 1: 1 – 1
Kombination 2: 1 – 2
Kombination 3: 1 – 3
…
Kombination 365: 1 – 365
es ist nun offensichtlich, dass sich dieses Spiel noch 364 Mal wiederholen lässt, indem jeweils der Geburtstag von Person A um eins verschoben wird. Also
Kombination 367: 2 – 1
Kombination 368: 2 – 2
…
Kombination 730: 2 – 365
Kombination 731: 3 – 1
…
Kombination 133.225: 365 – 365.
Mathematiker sind bekanntlich faule Leute und kürzen das ganze also ab. Die Anzahl der möglichen Geburtstags-Kombinationen für 2 zufällige Leute ist 365^2. Oder eben 133.225. Das schöne ist, dass sich so auch die Kombinationen für 3, 4 oder n Personen berechnen lassen (365^3, 365^4 oder 365^n).
Das nun der Zufall eintritt, dass beide am selben Tag (ohne Rücksicht auf den Jahrgang) Geburtstag haben ist dann ebenfalls purer Zufall. Den wir wieder nachbauen bzw. berechnen können.
Dazu bedienen wir uns eines „Tricks“ der bei der Berechnung von Wahrscheinlichkeiten regelmäßig angewandt wird. Wenn ich einen gewöhnlichen 6er-Würfel werfe, dann ist die Wahrscheinlichkeit eine „1“ zu werfen gleich 1/6. Das heißt umgekehrt aber, dass die Wahrscheinlichkeit NICHT eine „1“ zu werfen daher 1 – 1/6 = 5/6 (die Gegenwahrscheinlichkeit) ist. Der Grund für diesen Trick sei sogleich erklärt.
Wir wollen also schauen, wie viele Kombinationen es gibt, bei denen unsere beiden Personen NICHT den selben Geburtstag haben. Wenn Person A am 1. Tag geboren ist, dann bleiben für Person B 364 Tage über.
Kombination 1: 1 – 2
Kombination 2: 1 – 3
Kombination 3: 1 – 4
…
Kombination 364: 1 – 365
Wir können wieder weitermachen wie vorhin und sehen indem wir A einen Tag weiterrücken
Kombination 365: 2 – 1
Kombination 366: 2 – 3
Kombination 367: 2 – 4
…
Kombination 728: 2 – 365
Kombination 729: 3 – 1
Kombination 730: 3 – 2
Kombination 731: 3 – 4
…
Kombination 132.860: 365 – 364.
Insgesamt kommen wir also auf 365*364 (132.860) Kombinationen an denen die beiden NICHT den selben Geburtstag haben. Würden wir noch eine dritte Person in den Raum stellen, wären es 365*364*363. Dieses Muster lässt wie folgt verallgemeinern
365 * 364 * … * (365 – (n-1)).
Zurück zu unseren 2 Personen. Diese haben also in 132.860 von 133.225 möglichen Kombinationen NICHT den selben Geburtstag. Das entspricht der Wahrscheinlichkeit von
132.860 / 133.225 = 0,9973
und das sind 99,72%. Wir erinnern uns des „Tricks“ der Gegenwahrscheinlichkeit. Wenn sie in 99,72% NICHT den selben Geburtstag haben, dann ist der Rest die Wahrscheinlichkeit, dass sie am selben Tag geboren sind. Also 1 – 0,9973 = 0,0027 und somit mit einer extrem geringen Wahrscheinlichkeit von nur 0,27%.
Klarerweise könnte man auch argumentieren, dass es bei 2 Personen genau 365 Kombinationen gibt an denen beide Geburtstag haben (1-1, 2-2, …, 365-365). Dann käme man auf 365/133.225 = 0,0027 und somit direkt auf die entsprechende Wahrscheinlichkeit.
Sobald dann aber eine dritte Person hinzukommt, wird es hier bei der Zählung komplizierter da wir ja nur „mindestens 2 Geburtstage“ fordern und also alle möglichen Kombinationen („2 von 3 haben am selben Tag“ plus „3 von 3 haben am selben Tag“) untereinander berücksichtigen müssen. Dank Gegenwahrscheinlichkeit haben wir aber bereits nebenbei die allgemeinen Formeln aufgestellt, die weitere Rechnung ist daher denkbar einfach.
Hinweis: ab hier 😉
Für n = 23 Personen ergibt sich durch Einsetzen in unsere Formeln
(364 * 365 * … * 343) / 365^23 = 0,4927
und weiter
1 – 0,4927 = 0,5073
also 50,73% Wahrscheinlichkeit, dass zumindest 2 der 23 Personen am selben Tag Geburtstag haben! Wie man in der Grafik schön sehen kann, ist die Wahrscheinlichkeit bei 23 Personen erstmals über 50% und dann auch schnell bei fast 100% (ab 57 Menschen bereits über 99%). Klarerweise braucht es dann aber 366 Personen um die 100% wirklich zu erreichen und auszuschließen, dass man 365 verschieden Geburtstage bei 365 Personen hat. Was zwar möglich aber extreeeeem unwahrscheinlich wäre.
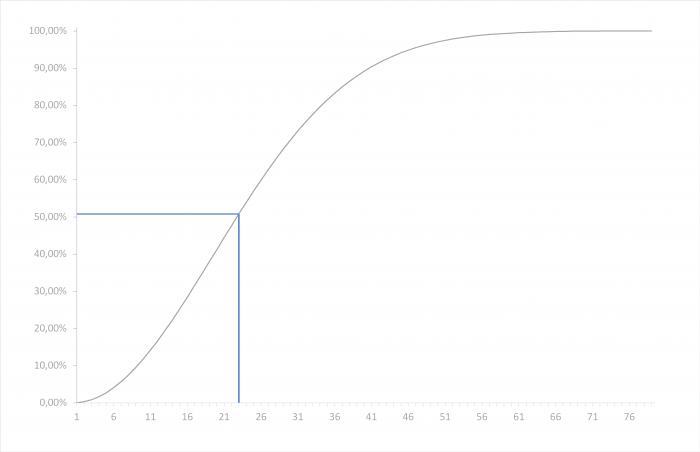
(x-Achse: Anzahl der Leute n, y-Achse: Wahrscheinlichkeit)
… und seine Auswirkungen
Nun stellen wir uns vor, dass wir es mit einem gewissen Hans Meier zu tun haben. Dieser Name wird in Österreich sehr sicher öfter vorkommen. Auf Herold.at gibt es dafür 7 Einträge. Und dann noch 37 weitere für Johann Meier. Und sollten wir uns beim Namen vertippt haben, so kommen wir für Johann Mayer bereits auf 260 Ergebnisse. Und dann wären da noch Maier und Mayr und Mair, …
Und Maier ist unter den häufigsten Familiennamen bloß der 17., Mayr der 21. in Österreich. Davor wären noch die Grubers, Hubers, Wagners, …
Mit dem Wissen um das Geburtstagsparadoxon können wir also davon ausgehen, dass es in Österreich eine beträchtliche Anzahl an Namensvetter mit dem selben Geburtstag gibt (oder mit fast gleichem Namen). Selbst die Wahrscheinlichkeit, dass es nicht nur der selbe Name und Tag sind sondern es auch noch das selbe Jahr ist, ist alles andere als klein.
Für ein Land wie die USA, mit fast 40x so vielen Einwohnern wie Österreich, ist die Wahrscheinlichkeit also noch viel höher. Dort heißen die Leute dann eben Catherine Taylor. Oder Cathrin oder Kathy oder Tyler…
Eine dieser Catherine Taylors aus Arkansas erhielt auf ihre sämtlichen Bewerbungen absagen. Ohne Begründung. Erst das Rote Kreuz war so „freundlich“ eine Begründung mitzuliefern. Sie wurde aufgrund ihrer Vorstrafe in der Datenbank der (extern beauftragten) Datenfirma abgelehnt. Dabei hatte sie keine Vorstrafe! Aber eine andere Frau mit gleichem Namen und gleichem Geburtstag. Seither ist sie damit beschäftigt solche Daten-Firmen juristisch zur Korrektur zu zwingen, denn sie läuft in ihrem Leben regelmäßig in automatisierte Ablehnungen. Doch dafür muss sie wissen wo die Fehler liegen und auf diese Auskunft hat sie selten Recht. Inzwischen wohnt sie in einem Haus das sie über ihre Schwester kaufen musste und nimmt Kredite über ihren Mann auf.
Und hier zeigt sich eine zweite eklatante Schwachstelle beim Einsatz von KI. Unternehmen die KI-Algorithmen entwickeln sind in der Regel Privatfirmen. Der Aufbau ihrer Algorithmen ist Betriebsgeheimnis. Und die Datenverarbeitung in der Regel eine Dienstleistung für einen Auftraggeber. Es ist also oft weder möglich zu erfahren warum eine konkrete Entscheidung so ausfiel, noch kann Einspruch gegen diese erhoben werden.
Dieses Beispiel ist nur die Spitze eines gewaltigen Eisberges beim (blinden) Einsatz der Kombination Big Data, Künstlicher Intelligenz und Machine Learning. Als extrem spannende und erkenntnisreiche Lektüre (mit vielen weiteren Beispielen) zu diesem Thema sei auf das Buch „Weapons of Math Destruction“ verwiesen.
Es steht außer Frage, dass Big Data (mit Künstlicher Intelligenz und Machine Learning) eine Vielzahl an positiven und hilfreichen Anwendungen finden werden. Aber blinde Technikgläubigkeit ist sicher fehl am Platz. Denn das obige Beispiel und viele andere mehr, zeigen deutlich, dass bei solchen fundamentalen Entscheidungen und Eingriffen in das Leben Transparenz ein absolutes Muss ist. Und das sich SoftwareentwicklerInnen, ProgrammiererInnen, TechnikerInnen und IT-Konzerne sehr wohl mit Ethik beschäftigen müssen. Und es faire Einspruchmöglichkeiten gegen automatisierte Entscheidungen geben muss.
* Anm.: In der Realität sind nicht alle Geburtstermine gleich wahrscheinlich, so werden z.B. im Sommer mehr Kinder geboren als im Winter. Dies ist aber nicht von tragischem Einfluss. Auch der hier vernachlässigte Schalttag führt zu keiner Änderung der Ergebnisse. Aber das auszuführen würde zu weit führen 😉


Ein Kommentar
Kommentare sind geschlossen.