… oder: warum wir zum Messen verschiedene Skalen verwenden (sollen)
„Bayerns Bauern [haben] in diesem Jahr Blühflächen in der Größenordnung von rund 12.000 Fußballfeldern geschaffen“ und „Wenn der Ostsee gefüllt ist, fasst er so viel Wasser wie etwa zwei Milliarden Badewannen“ sind zwei der unzähligen Schlagzeilen, in denen diese beiden „Maßeinheiten“ herhalten müssen. Doch warum werden Flächen überhaupt in Fußballfelder umgerechnet und Volumen (oder Volumina) in Badewannen?
Maßeinheiten mögen zwar normiert sein, sind aber zu einem gewissen Grad doch „willkürlich“ festgelegt. So gibt es weltweit nach wie vor parallele „alternative“ Maßeinheiten zu jenen, im Système international d’unités (SI) international festgelegten (z.B. Fuß und Meilen für Länge oder Celsius und Fahrenheit für Temperatur). Sie alle eint die Idee gewisse (abstrakte) Größen verständlich und miteinander vergleichbar zu machen (war es gestern kälter als heute?). Sobald allerdings die Höhe des Eiffelturms (324 Meter) mit dem Durchmesser einer Euro-Münze (2,3 Centimeter) oder der Dicke eines Haares (ca. 0,2 Millimeter) gemessen werden sollen, wird es jedoch schwierig. Die Reihenfolge ist offensichtlich, aber die genaue Messung alles andere als einfach. Während mit einem Maßband die Euromünze bequem vermessen werden kann, wird man damit weder beim Eiffelturm noch beim Haar weiterkommen. Das Maßband hat schlichtweg eine falsche Skalierung für die (Mess-) Probleme!
Der Hausverstand alleine sagt uns, dass wir zum Messen von Objekten unterschiedlicher Größenordnungen unterschiedliche Skalierungen brauchen. Für das Längenmaß sind bereits 3 verschiedene benutzt worden: Meter, Centimeter und Millimeter. Die sind nichts anderes als „Unterteilungen“ voneinander. 1m = 100cm und 1cm = 10mm. Und nach oben hin ist 1km = 1000m. Ein Kilometer ist also nichts anderes als 1.000.000mm in Worten: eine Million Millimeter. Die Distanz zwischen Eisenstadt und New York (Luftlinie 6851 km) wird im Alltag niemand mit 6.851.000.000 Millimeter (bzw. 6,85 Milliarden Millimeter) angeben. Doch es gibt im Alltag oft Bereiche, in denen wir Werte aus einem (sehr) breiten Spektrum miteinander vergleichen müssen. Oft mit unterschiedlicher Genauigkeit.
Zum Beispiel beim Autofahren. Während in der 30er-Zone bloß 10km/h mehr schon zu einer Strafe führen, kann es mir auf der Deutschen Autobahn (straftechnisch) egal sein, ob ich nun 130, 140 oder 220km/h fahre. Tachometer berücksichtigen diesen Umstand dementsprechend.

Würde dieser Tacho von 50 bis 100 den selben Winkel haben wie zwischen 0 und 50, dann würde auf der 12:00 Position 100 km/h stehen. Werden die 0 – 140 verdoppelt, würden auf der 6:00 Position erst 280 angeschriben sein. So aber ist es möglich, dass wir sowohl im Ortsgebiet als auch auf der Landstraße eine präzise Einschätzung der Geschwindigkeit haben. Ab 130 hingegen wird die Information zu einem Näherungswert – und da sollten die Augen ohnehin eher auf die Straße gerichtet sein. (Warum der „analoge“ Zeiger-Tachometer übrigens die perfekte Wahl für den Tachometer ist, darum geht es in einem der nächsten Beiträge).
Auch beim Messen der Temperatur macht es einen Unterschied ob ich die Außentemperatur oder die Körpertemperatur messe. Für erstere reichen 1-2 Grad Genauigkeit (außer es droht Glatteis), aber 41°C und 43° Körpertemperatur machen einen riesigen Unterschied. Es braucht also auch hier unterschiedliche Skalen auf den jeweiligen Thermometern.
Ein ähnliches Problem stellt sich, wenn die Bevölkerungszahlen von Liechtenstein (38.000), Österreich (8.773.000), Deutschland (82.457.000), Indonesien (255.462.000) und China (1.379.000.000) auf einer Skala (z.B. in einem Diagramm) verglichen werden sollen (Quellen: Wikipedia).

In einem Balkendiagramm mit einer „normalen“ y-Achse sind die Größenunterschiede – so wie bei Eifelturm, Münze und Haar – klar erkennbar, aber das Ablesen der einzelnen Werte ist praktisch unmöglich. Die „normale“ Skalierung der y-Achse wird auch lineare Skalierung genannt. Das bedeutet, dass zwischen den Werten 1 und 10 im Diagramm der selber Abstand herrscht wie zwischen 10.001 und 10.010. Es gibt jedoch noch viele andere Möglichkeiten der Skalierung.
Eine der häufigsten Alternativen ist die logarithmische Skalierung. Sie hat ihren Namen vom Logarithmus, einer mathematischen Funktion, mit der sehr stark wachsende Reihen von Zahlen übersichtlich dargestellt werden können. Der Vollständigkeit halber sei noch erwähnt, dass es unterschiedliche Arten des Logarithmus gibt (genauer: Logarithmen mit unterschiedlicher Basis). Wir beschränken uns auf den „dekadischen“ (mit Basis 10). Verwendet man die (klassische) logarithmische Skalierung für ein Diagramm, dann entspricht jeder Skalenstrich einer Zehnerpotenz (Salopp: eine Null mehr). Der Abstand zwischen 1 und 10 ist daher gleich groß, wie jener von 10 und 100 oder 10.000 und 100.000.
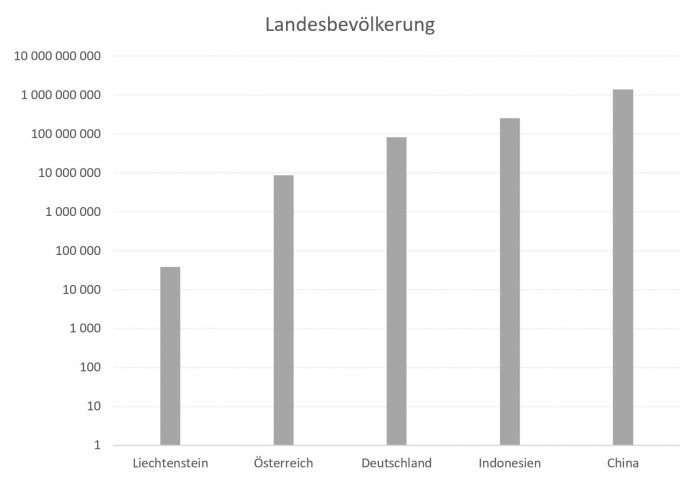
Wird diese Skala verwendet um obige Einwohnerzahlen darzustellen, so sind nun alle Länder klar erkennbar und ihre Größe kann abgelesen werden. Da die Skala aber nicht linear ist, sondern eben logarithmisch, ist sie „verzerrt“. Österreich und das etwa 10x so großen Deutschland trennt ein Skalenstrich (also eine 10er-Potenz). Und dass Chinas Balken doppelt so hoch ist wie jener von Liechtenstein bedeutet nicht, dass China zweimal so viele Einwohner hat wie Liechtenstein, sondern „hoch 2-mal“ so viele – also quadratisch so viele (38.000^2 = 1,444 Milliarden).
Klar ist diese Lesart von Diagrammen anfangs gewöhnungsbedürftig, aber richtig angewandt ermöglicht sie den Blick auf das Wesentliche zu lenken – ähnlich dem der Tacho im Auto. Erst so lassen sich in ihre Größenordnung stark unterschiedliche Objekte miteinander vergleichen. Zum Beispiel erkennt man, dass die Anzahl an NobelpreisträgerInnen eines Landes offensichtlich nicht von der Einwohnerzahl abhängt (halte den Mauszeiger auf einen Punkt um Details zu sehen).
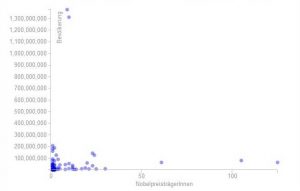
Im gleichen Diagramm ist bei einer linear (normal) skalierten y-Achse nicht viel zu sehen. Die „mittelgroßen“ Länder sind eine einzige undurchsichtige Punktwolke, da Indien & China die y-Achse „verzerren“ (eine Erklärung zum Scatterplot findest du in diesem Beitrag.)
Das Schöne am Logarithmus ist, dass mit ihm viele Phänomene der Natur beschrieben werden können. Das ist auch der Grund, warum wir im Alltag regelmäßig (unwissentlich) mit logarithmischen Skalen zu tun haben. So ist die Dezibel-Skala, mit der der Schalldruck gemessen wird, logarithmisch, oder auch die Richterskala für die Stärkeeinteilung von Erdbeben. Und selbst das Wachstum von Schneckenhäusern und Sonnenblumen wird durch logarithmische Spiralen beschrieben.
Nachbemerkung: Eine gut gewählte Skalierung kann viel zur Lesbarkeit von Diagrammen beitragen. „Falsch“ gemacht, können sie Diagramme jedoch unlesbar machen oder (absichtlich) manipulieren. Aber mehr dazu in eine der nächsten Beiträge…
Titelbild/Tacho:
Danke an Sébastien Launay fürs Zurverfügungstellen des Tacho-Fotos unter der CC-by-2.0 Lizenz.


Ein Kommentar
Kommentare sind geschlossen.