In der Wissenschaft gehören Scatterplots (deutsch Streudiagramm) zum Standardwerkzeug. In der „normalen“ Medienlandschaft sind sie hingegen kaum anzutreffen. Woran liegt das? Ein Grund dafür könnte ihre vermeintliche Komplexität sein. Doch sind sie wirklich kompliziert zu verstehen? Und was für Vorteile haben sie überhaupt?
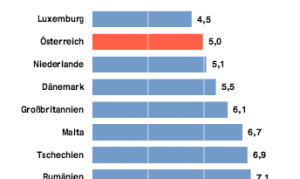
Wenn Grafiken/Diagramme zum Einsatz kommen, so wird in der Regel nur eine Größe (Kennzahl) dargestellt. Zum Beispiel wird die Arbeitslosenquote der EU-Länder gegenübergestellt (Quelle: WKO).
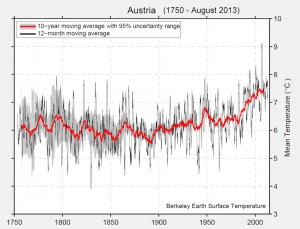
Oder es wird eine Größe (Kennzahl) im Zeitverlauf betrachtet, etwa die Entwicklung der Durchschnittstemperatur an einem gewissen Ort. Hier zum Beispiel die Jahresmitteltemperatur (schwarze Linie) und der Zehnjahresmittelwert (rot) für Österreich (Quelle: Wiki).
Diese Art der Darstellungen ist vollkommen plausibel sowie einem breiten Publikum bekannt und geläufig. Sie ermöglichen es eine Größe in Relation zu setzen. Im ersten Beispiel um zu vergleichen wie verschiedene Länder dastehen, im zweiten um eine Entwicklung im Zeitverlauf zu beobachten. Diese Darstellungen erlauben es aber eben nur eine einzige Größe darzustellen.
Für die Beschreibung eines Phänomens mag das Ausreichen (etwa um zu zeigen, dass Österreich eine niedrige Arbeitslosigkeit hat). In einer zunehmend komplexen und vernetzten Welt, ist es jedoch oft nicht möglich die Wirklichkeit mit einer einzigen Kennzahl zu erklären. Denn oft ist es das Zusammenspiel von mehreren Faktoren (welche durch Kennzahlen beschrieben werden) das es ermöglicht ein Phänomen zu erklären.
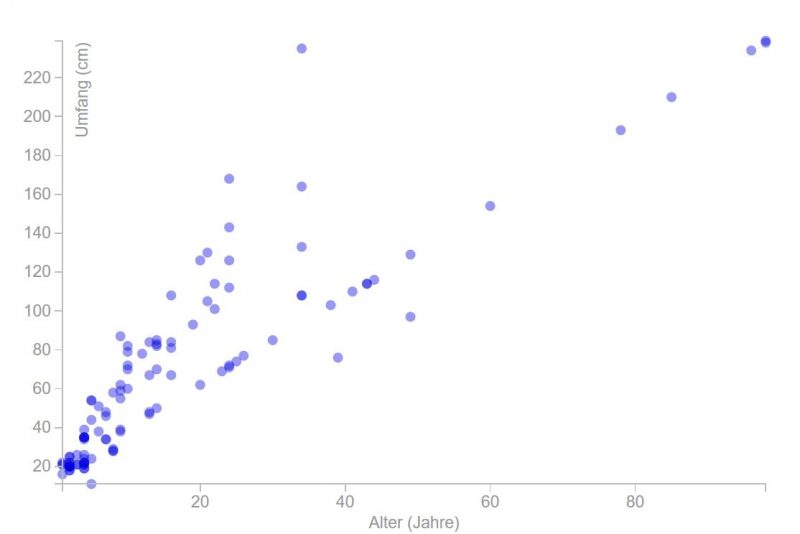
Der Scatterplot hingegen ermöglicht es, zwei Kennzahlen eines Objektes miteinander in Relation zu bringen. Betrachten wir dazu ein – zugegebenerweise sehr simples – Beispiel: Baumwachstum. Im Folgenden wird eine zufällige Auswahl von 111 Bäumen verwendet, welche in der Stadt Wien wachsen (halte den Mauszeiger auf einen Punkt um Details zu sehen).
Nun ist die Erkenntnis, dass ältere Bäume einen größeren Stammumfang haben keine wirklich welterschütternde Neuigkeit. Aber das Beispiel zeigt schön auf, dass es einen (relativ linearen) Zusammenhang zwischen den beiden betrachteten Größen (Alter und Umfang) gibt. So könnte mensch zum Beispiel annehmen, dass die Anzahl an Nobelpreisträgern von der Einwohnerzahl eines Landes abhängt. Wie folgender Scatterplot zeigt, ist dies aber nicht der Fall (halte den Mauszeiger auf einen Punkt um Details zu sehen).
Auf der y-Achse (in vertikaler Richtung) ist die Bevölkerung der Länder aufgetragen und auf der x-Achse (horizontal) die Anzahl der NobelpreisträgerInnen. Die y-Achse ist eine logartithmisch skalierte (mehr zur Skalierung gibt es in einem der nächsten Beiträge), da sonst der Abstand zwischen den Färöer-Inseln (48.000 Einwohner) und China (1,4 Milliarden) zu groß wäre und das Gros der mittelgroßen Staaten zu dicht zusammengeklebt wäre. Außerdem wurden die USA weggelassen, da sie mit 353 Nobelpreisen fast 3x so viele halten wie Großbritannien – das Land mit den zweitmeisten. Dies könnte wieder durch eine logarithmische Achse ausgeglichen werden, ist in diesem Fall jedoch nicht wirklich hilfreich (Quelle: Wiki).
Im Scatterplot wird ersichtlich, dass es offensichtlich nicht (nur) die Größe eines Landes ist, welche die Anzahl an Nobelpreisen beeinflusst. So hat Österreich bei 8,5 Mio. Einwohnern 21 Preise, während Argentinien, Spanien, Südafrika, Polen bei etwa 5-facher Einwohnerzahl auf 5-12 PreisträgerInnen kommen.
Es ist jedoch äußerste Vorsicht geboten, wenn versucht wird mit Scatterplots Ursache und Wirkung, bzw. Zusammenhänge zu erkennen! Mehr zu dem Thema gibt es im folgenden Beitrag, wo es um Kausalität und Korrelation geht.

2 Kommentare
Kommentare sind geschlossen.