Das Schöne am Datenjournalismus ist es, dass er Geschichten erzählen kann die sonst unentdeckt blieben. Dass er aus Daten Information und Fakten extrahieren kann, welche dann in eine Story münden. Das macht ihn aber auch tricky. Denn um Daten korrekt zu interpretieren bedarf es eines entsprechenden Vorwissens.
Was passieren kann, wenn nicht umsichtig gearbeitet wird und der Datenjournalismus in den Verruf der „Lügenpresse“ gerät, wird in diesem Blogartikel erörtert.
Ein oft gemachter Fehler ist das verwechseln von Korrelation und Kausalität – um die es, wie letztens versprochen, in diesem Artikel geht. Die beiden Begriffe sind zugegebenermaßen etwas sperrig und eher Statistikern und Mathematikern geläufig. Korrelation bedeutet, dass zwei (oder mehrere) „Eigenschaften“ in einer Beziehung zueinander stehen. Um beim Baumbeispiel vom letzen Mal zu bleiben: der Stammumfang und das Alter eines Baumes stehen in einer Beziehung zueinander. Steigt eine Eigenschaft, so steigt auch die andere. Das Problem mit der Korrelation ist, dass sie oft mit Kausalität verwechselt wird.
Kausalität bedeutet, dass eine Eigenschaft die andere beeinflusst. Etwa, dass ein Baum mit zunehmendem Alter einen immer dickeren Stamm besitzt. Umgangssprachlich formuliert: eine Eigenschaft misst die „Ursache“ (Alter) und die andere deren „Wirkung“ (Wachstum). In dem Fall werden Biologen wohl nicht widersprechen, dass diese beiden Eigenschaften (auch Merkmale genannt) tatsächlich voneinander abhängen – also ein Kausalzusammenhang besteht. Wenn zwischen Merkmalen ein Kausalzusammenhang besteht, so darf erwartet werden, dass diese korrelieren.
Leider (oder zum Glück) gilt der Umkehrschluss aber nicht. Eigenschaften können zufällig korrelieren ohne dass ein Ursache-Wirkung Zusammenhang besteht. Eines der berühmten Statistikbeispiele hierfür ist jenes, dass viele Störche für viele Babys sorgen (hat es unter anderem sogar in die Zeit geschafft). Ein anderes schönes ist der Zusammenhang von Globaler Erwärmung und der sinken Anzahl Piraten. Dieses Beispiel wird von Pasterfaris für die „Untermauerung“ ihrer „Religion“ verwendet und hat es auch schon in die Forbes geschafft.
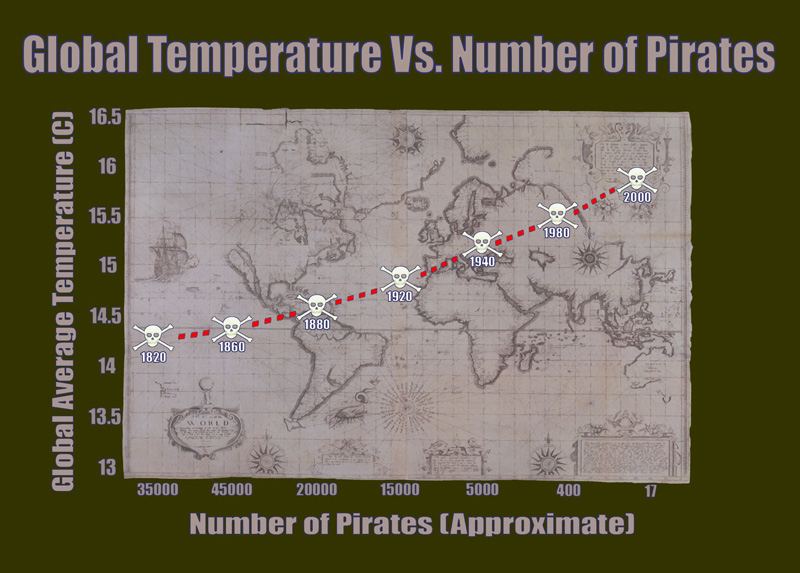
Auch wenn die Ölindustrie vermutlich ganz gerne die Schuld für die Erderwärmung auf die sinkende Zahl an Piraten schieben würde und sich vielleicht auch mancheineR darüber freut, dass einem Babymangel durch mehr Störche begegnet werden kann, so erscheint es doch recht unwahrscheinlich, dass diese Phänomene in Kausalzusammenhängen stehen.
Mittels Scatterplots lassen sich zwar schön Korrelationen zeigen, also „Beziehung“ der Größen. Aber, wie oben erwähnt, eine Korrelation ist noch kein Beleg für einen Zusammenhang. Im Fall der Piraten werden zwei beliebige Größe miteinander verkuppelt. Mehr Beispiele für solche, beliebige Verkupplungen gibt es hier (Liniendiagramme). Im Storchbeispiel ist die Sache schon ein wenig anders. Hier gibt es einerseits den lange tradierten Mythos vom Kinderbringen – und einen tatsächlichen Zusammenhang.
Dieser Zusammenhang ist jedoch weniger, dass Störchen tatsächlich Kinder bringen. Vielmehr gibt es eine gemeinsamen Erklärung für beide Effekte. (Diese Zwischenvariable wird in der Statistik als „intervenierende Variable“ bezeichnet.) Also einen externen Grund dafür, dass sowohl die Anzahl an Kindern als auch an Störchen höher oder niedriger ist. Zum Beispiel der Verbauungs-, Urbanisierungs- bzw. Industrialisierungsgrad einer Gegend. Frauen die in Städten leben, haben normalerweise weniger Kinder als jene in ländlichen Gegenden und Störche leben bevorzugt in ländlichen Regionen – und nicht auf Hochhäusern oder in Betonwüsten.
Stellt sich also die Frage, wie erkannt werden kann ob Merkmale nur zufällig korrelieren oder tatsächlich kausal zusammenhängen. Für Journalistinnen ist die Antwort vermutlich unbefriedigend, für WissenschafterInnen hingegen beruhigend: es ist schwer.
Statistisch ist es möglich Hypothesen auf ihre Signifikanz zu prüfen. Also etwa „in Regionen mit mehr Störchen leben mehr Kinder“. Die Hypothese könnte aber genauso gut lauten „mehr Störche führen zu mehr Kindern“. Beide werden – mit gleichen Daten – gleich beantwortet werden. Falls der Verdacht besteht, dass es eine Zwischenvariable gibt, so kann statistisch überprüft werden, ob dies der Fall ist oder nicht. Es obliegt aber den Forscherinnen, dass sie mit ihrem Wissen und ihrer Forschung diese Zwischenvariablen identifizieren und ihre Hypothesen vernünftig formulieren.
Für Nicht-Experten muss der Rat also lauten beim „Entdecken“ von (scheinbaren) Zusammenhängen sehr vorsichtig zu sein. Und im Zweifel Expertinnen und/oder Statistikerinnen zu Rate zu ziehen.

Ein Kommentar
Kommentare sind geschlossen.